Learning Modules Hide
Hide
- Chapter 1: Basics of Derivatives
- Chapter 2: Futures and Forwards: Know the basics – Part 1
- Chapter 3: Futures and Forwards: Know the basics – Part 2
- Chapter 4: A Complete Guide to Futures Trading
- Chapter 5: Futures Terminology
- Chapter 6 – Futures Trading – Part 1
- Chapter 7 – Futures Trading – Part 2
- Chapter 8: Understand Advanced Concepts in Futures
- Chapter 9: Participants in the Futures Market
- Chapter 1: Introduction to Derivatives
- Chapter 2: Introduction to Options
- Chapter 3: An Options Trading Course for Option Trading Terminology
- Chapter 4: All About Options Trading Call Buyer
- Chapter 5: All About Short Call in Options Trading
- Chapter 6: Learn Options Trading: Long Put (Put Buyer)
- Chapter 7: Learn Options Trading: Short Put (Put Seller)
- Chapter 8: Options Summary
- Chapter 9: Learn Advanced Concepts in Options Trading – Part 1
- Chapter 10: Learn Advanced Concepts in Options – Part 2
- Chapter 11: Learn Option Greeks – Part 1
- Chapter 12: Option Greeks – Part 2
- Chapter 13: Option Greeks – Part 3
- Chapter 1: Learn Types of Option Strategies
- Chapter 2: All About Bull Call Spread
- Chapter 3: All About Bull Put Spread
- Chapter 4: Covered Call
- Chapter 5: Bear Call Spread
- Chapter 6: Understand Bear Put Spread Option Strategy
- Chapter 7: Learn about Covered Put
- Chapter 8: Understand Long Call Butterfly
- Chapter 9: Understand Short Straddle Strategy in Detail
- Chapter 10: Understand Short Strangle Option Strategy in Detail
- Chapter 11: Understand Iron Condor Options Trading Strategy
- Chapter 12: A Comprehensive Guide to Long Straddle
- Chapter 13: Understand Long Strangle Option Strategy in Detail
- Chapter 14: Understand Short Call Butterfly Option Trading Strategy
- Chapter 15: Understanding Protective Put Strategy
- Chapter 16: Protective Call
- Chapter 17: Delta Hedging Strategy: A Complete Guide for Beginners
Chapter 13: Option Greeks – Part 3
If you have traded in Options, you may have heard about Theta, Vega and Rho, but perhaps you don't know what they are and how they can help you in Options trading. So read on, and we will explain what these Option Greeks mean and how they can help you evaluate the price of an Option.
Theta
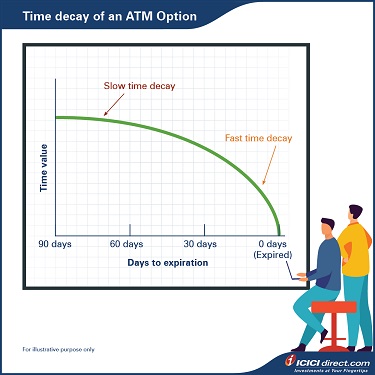
Theta indicates how time decay (reduction in time to expiration) impacts the Option premium. The value of the Call Option declines as the contract approaches maturity, assuming all other things remain the same. That is also true for most Put Options.
Theta or time decay of an Option is not linear. Theoretically, the decay rate will tend to increase as the contract reaches near expiry or the time to expiration decreases. Therefore, the amount of fall due to Theta seems to be gradual and accelerates as the Option approaches maturity. On expiry, time value becomes zero and Options trade only at intrinsic value.
If ABC Ltd. is trading at Rs. 500 and a 500 strike call was trading at Rs. 30 with a Theta of 1; an investor would anticipate that Option to lose about Re. 1 per day, assuming no other change. Thus, with one day left until expiration, the Theta will be equal to the entire value of the time value portion left in the Option premium.
In the example given below, the Theta of Nifty strike price of 23,200 is -14. Therefore, the Option value will fall by Rs. 14 each passing day due to Theta if all other factors remain the same.

*Image is for illustrative purpose only; such representations are not indicative of future results
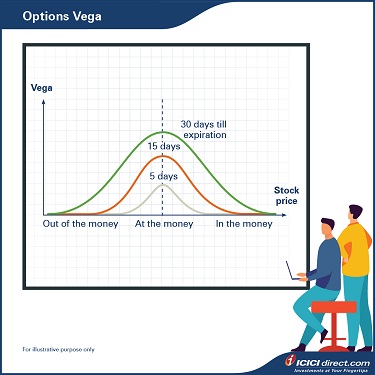
Vega
Vega calculates the extent to which the Option premium would change because of changes in market implied volatility. Implied volatility will increase with the uncertainty in the market. The higher the volatility, the higher is the price of both Call and Put Options. So, Vega is positive for both Call and Put Options.
- For example, a 1-month Option on stock XYZ (spot price Rs. 50) with Rs. 50 strike price has a Vega of 0.2. In other words, the Option's value might go up by Rs. 0.2 if implied volatility increases by one point, the Option's value might go down by Rs. 0.2 if implied volatility decreases by one point.
Options with a longer expiry period are more affected by volatility and have a higher Vega. Similarly, contracts near strike price or ATM Options have higher Vega and Vega falls when the Option moves away from the strike price.
Please note that Vega and implied volatility can be changed without any change in the price of the underlying stock price. Therefore, it would be best not to look at the Vega in isolation because volatility will also impact the Delta and Gamma. With an increase in volatility, Delta and Gamma also tend to move. Therefore, we need to see the combined impact of Greeks on the Option pricing.
You can find the value of Option Greeks of a particular strike price from the Price Calculator available under the Option Express tab on ICICIdirect.com

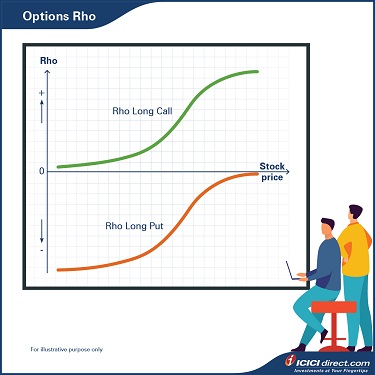
Rho
Rho calculates the extent to which the Option premium would change because of a change in the risk-free rate.
But why do interest rates have an impact on Option pricing? We assume that a trader doesn't have their own money and needs to borrow money to purchase an Option. Similarly, if he sells the Options, he will use the money to earn an interest income by investing in a risk-free instrument.
Let's understand this with an example:
Assume you are bullish on a share for a short period and expecting a rise in the price in 3 months. Either you can buy the shares, or you can buy a Call Option. If You decide to buy 2000 shares whose current price is Rs. 100, you require Rs. 2000*100= Rs. 2,00,000. If you borrow this amount at a 5% p.a. risk-free rate, your interest outgo will be Rs. 2,00,000*5%*3/12 = Rs. 2,500
If you buy a Call Option of that stock for Rs. 10, your profit potential will remain the same, but you need to borrow only 2000*10 = Rs. 20,000 and the interest outgo will be 20,000*5%*3/12 = Rs. 250
It means there is a saving in interest outgo of Rs. 2500-250 = Rs. 2250 if a person buys the Call Option. So, if the interest rate rises, this will lead to more savings, which would be higher for long-term Call Options.
Does the scenario remain the same for Put Options?
For Put Options, the scenario would be reversed. If you are bearish about a stock, you have two options. Either you can short the stock or buy the Put Options on the stock.
If you short the stock, you will receive the amount and you can earn the interest. If we go with the above example, you will receive the interest income of Rs. 20,000 in this case. Suppose a Put Option is available in the market at Rs. 10. In that case, you need to borrow the amount equivalent to the premium paid, i.e., Rs. 20,000 and need to pay the interest of Rs. 250. A rise in the interest rate is profitable if a trader uses to short the stock and he will be able to earn higher interest. But for the Put holder, it will lead to higher interest outgo. So rising interest will have a negative impact on the Put Option pricing. So, we can conclude the following:
- Change in interest rates impacts the longer Option more than the near to expiry Options.
- The value of Call Options increases as the risk-free rate increases (the Call Option Rho is positive).
- Rho is positive for long calls and increases with the price of the stock.
- The Put Options value decreases as the risk-free rates increases (the Rho of a Put Option is negative).
- Rho is negative for long puts and approaches zero as the stock price increases.
For example, assume the current risk-free rate is 5%. If a Call Option has a Rho of 0.5 and the interest rate suddenly goes up to 6%, the Option premium would rise by Rs. 0.5. Conversely, if a Put Option has a Rho of -0.5, the Put premium would decline by Rs. 0.5.
Option Greeks summary
Summary
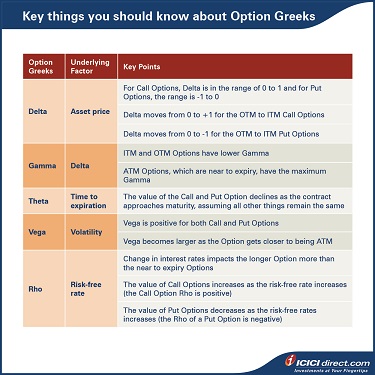
- Theta indicates how a reduction in time to expiration impacts the Option premium.
- Vega calculates the extent to which the Option premium would change because of changes in market implied volatility.
- Rho calculates the extent to which the Option premium would change because of a change in the risk-free rate.
This brings us to the end of the Options module. Now, you should know what an Option means, different types of Options and how to trade in these. To learn about the Option strategies, you can refer to our module on the Option strategies.
Disclaimer:
ICICI Securities Ltd. ( I-Sec). Registered office of I-Sec is at ICICI Securities Ltd. - ICICI Venture House, Appasaheb Marathe Marg, Prabhadevi, Mumbai - 400 025, India, Tel No : 022 - 6807 7100. I-Sec is a Member of National Stock Exchange of India Ltd (Member Code :07730), BSE Ltd (Member Code :103) and Member of Multi Commodity Exchange of India Ltd. (Member Code : 56250) and having SEBI registration no. INZ000183631. Name of the Compliance officer (broking): Mr. Anoop Goyal, Contact number: 022-40701000, E-mail address: complianceofficer@icicisecurities.com. Investments in securities market are subject to market risks, read all the related documents carefully before investing. The contents herein above shall not be considered as an invitation or persuasion to trade or invest. I-Sec and affiliates accept no liabilities for any loss or damage of any kind arising out of any actions taken in reliance thereon. Such representations are not indicative of future results. The securities quoted are exemplary and are not recommendatory.
Option features are offered by ICICI Securities. Any complaint / dispute pertaining to the same would not be entertained by Stock Exchanges.

Track your application







COMMENT (0)